- What are the elements of communication systems? Explain with classifications of communication systems
- What is the Frequency Spectrum of Communication Systems? Why Modulation is necessary in wireless transmission?
- What is Amplitude Modulation? Complete Mathematical Derivation of AM Wave
- What is the Importance of Side Bands in Amplitude Modulation? What are the types of AM?
- What is Frequency Modulation? Explain the process with diagram and mathematical analysis
- What is Satellite communication? Give Detailed explanation with diagram and mathematical analysis
In this topic, first we will understand the process of amplitude modulation and then write the mathematical derivation of AM wave. I suggest you to take a pen and paper while reading this article and write down each step of the derivation while reading.
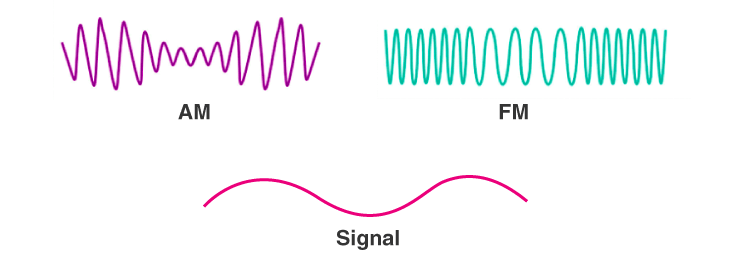
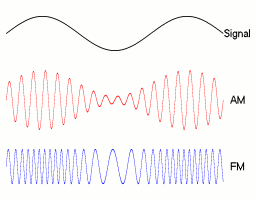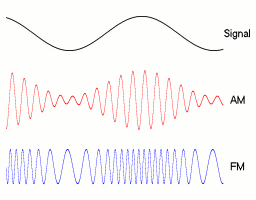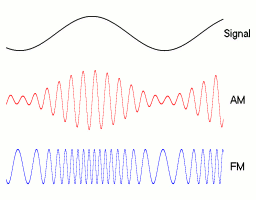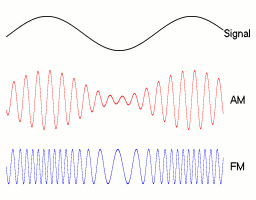
Definition: Amplitude modulation is defined as the process, in which the amplitude of carrier signal is changed in accordance with the amplitude of modulating signal. To produce AM wave, a carrier signal of frequency fc is mixed with another low frequency modulating signal of frequency fm in a circuit known as amplitude modulator.
Suppose carrier signal is given by –
ec = Vc.sin(ωc).t … (1)
And the modulating signal is given by –
em = Vm.sin(ωm).t … (2)
Now when they are mixed in amplitude modulator circuit, AM wave is produced. The peak amplitude of this AM wave is given by –
A = Vc + em = Vc + Vm.sin(ωm).t … (3)
Now let ‘m’ be the ratio of peak amplitude of modulating signal to peak amplitude of carrier signal. The value of ‘m’ is known as modulation index –
m = Vm / Vc i.e. Vm = m.Vc
Putting this value of Vm in equation (3), we get –
A = Vc + m.Vc.sin(ωm).t = Vc (1 + m.sin(ωm).t ) … (4)
Now the equation of AM wave is given by –
emod = A.sin(ωc).t … (5)
where, emod = instantaneous amplitude of amplitude modulated (AM) wave
Putting the value of equation (4), in equation (5), we get –
emod = (Vc (1 + m.sin(ωm).t )).sin(ωc).t … (6)
By solving equation (6), we get –
emod = Vc.sin(ωc).t + m.Vc ((sin(ωc).t ).(sin(ωm).t )) … (7)
Applying trigonometric rule, finally we get –
(sin(x).sin(y)) = ½ sin(x – y) – ½ sin(x + y). So applying this rule to equation (7), finally we get –
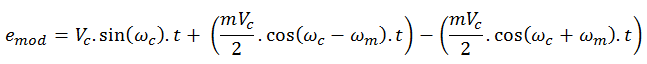
Bandwidth of AM Wave
The above given final equation of AM wave consists of three components –
Original i.e. unmodulated carrier frequency: ωc = 2π.fc
The Lower Side Band (LSB): ωc – ωm = 2π.( fc – fm )
And the Upper Side Band (USB): ωc + ωm = 2π.( fc + fm )
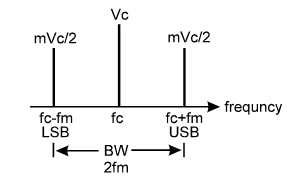
The difference of USB and LSB is called as the bandwidth –
BW = (2π.( fc + fm )) – (2π.( fc – fm )) = 2fm
Important Definitions
These are the two important definitions in order to understand the next topic of importance of sidebands in AM process –
Modulation index (m)
It is defined as the ratio of peak amplitude of modulating signal to the peak amplitude of carrier signal.
m = Vm / Vc
Percentage modulation (M)
When modulation index ‘m’ is multiplied with 100, that is expressed in percentage, it is called as percentage modulation M.
M = m × 100 = ( Vm / Vc ) × 100