- Thevenin’s Theorem
- Norton’s Theorem
- Superposition Theorem
- Maximum Power Transfer Theorem
- Millman’s Theorem
- Simple Calculation Methods to Solve Problems of Mesh Analysis
In mesh analysis any resistive, inductive or capacitive circuit can be analysed to obtain current in any branch of the circuit. We shall use one simple example to understand mesh analysis.
Note that in order to understand the Mesh Analysis in details, you must first read and prepare the topics of Kirchhoff’s Current Law (KCL) and Kirchhoff’s Voltage Law (KVL) in the series of Fundamentals of Electricity.
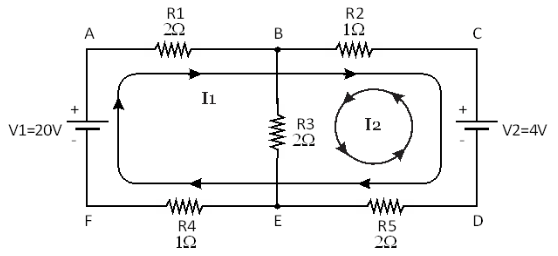
Consider the following circuit. Here there are three resistors and two batteries used in the circuit. We have to calculate the current flowing through resistor R3 when both batteries are connected in the circuit.
To find out the current in R3 we shall consider two current loops. The first current I1 is flowing clockwise in the loop A-B-E-F-A through R1, R2 and the battery V1.
The second current I2 is flowing anti-clockwise in the loop C-B-E-D-C through R2, R3 and the second battery V2.
It means there are two currents I1 and I2 flowing through R3. Now we shall write equations of I1 and I2 as follows:
Equation for the loop A-B-E-F-A
I1.R1 + R3.(I1 + I2) – 4 = 0
Putting the values of resistors we get –
2I1 + 2(I1 + I2) – 4 = 0
i.e. 4.I1 + 2.I2 = 4
So 2.I1 + I2 = 3 ……(1)
Equation for the loop C-B-E-D-C
I2.R2 + R3.(I1 + I2) – 8 = 0
Putting the values of resistors we get –
1.I2 + 2.(I1 + I2) – 8 = 0
i.e. 2.I1 + 3.I2 = 8 ……(2)
Considering equations (1) and (2) as simultaneous equations, we get –
2.I1 + I2 = 2 ……(1)
2.I1 + 3.I2 = 8 ……(2)
Multiplying equation (2) with. (–1) we get –
2.I1 + I2 = 2 ……(1)
–2.I1 + (–3.I2) = –8 ……(2)
i.e. (–2.I2) = –6A
So we get I2 = 3A
Putting this value in equation (1), we get the value of I1 –
I1 = –0.5A
The negative (–) sign of I1 shows that the direction of I1, which we had considered, is wrong. The current I1 is actually flowing in opposite direction i.e. in anticlockwise direction in the circuit.
So finally the total current flowing through R3 will be the sum of I1 and I2 –
IR3 = I1 + I2 = 3A + (–0.5A) = 2.5A
Exercise
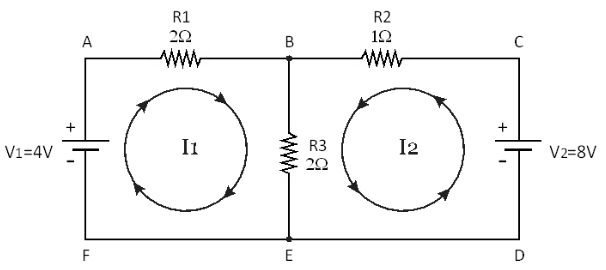
- Using Mesh Analysis, calculate the total current through R2 in the circuit given below. (Ans: 3A)
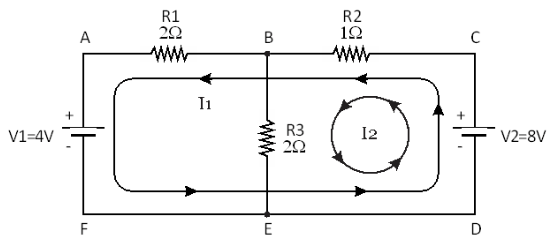
- Calculate the total current through R5 in the circuit using Mesh Analysis. (Ans: 0.96A)